Объяснение линейной регрессии
О линейной регрессии простыми словами
В этой статье я объясню линейную регрессию простыми словами. Это можно считать статьей "Линейная регрессия для чайников", однако мне никогда не нравилось это выражение.
Прежде чем мы начнем, предлагаем вам несколько дополнительных ресурсов, которые помогут вам взлететь по карьерной лестнице в Machine Learning:
Для получения обучающих ресурсов перейдите на сайт Яндекс Практикум!
Линейная регрессия в машинном обучении
В мире машинного обучения линейная регрессия - это вид параметрической регрессионной модели, которая делает прогноз путем взятия средневзвешенного значения входных характеристик наблюдения или точки данных и добавления константы, называемой членом смещения.
Это означает, что простые модели линейной регрессии - это модели, которые имеют определенное фиксированное количество параметров, зависящих от количества входных признаков, и выдают числовое предсказание, например, стоимость дома.
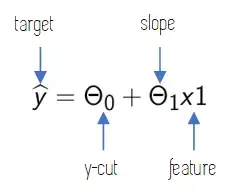
Общая формула линейной регрессии выглядит следующим образом:
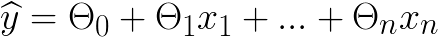
ŷ - значение, которое мы прогнозируем.
n - количество признаков наших точек данных.
xi - значение первого признака.
Θi - параметры модели, где Θ0 - член смещения.
Все остальные параметры - это веса для признаков наших данных.
Если бы мы хотели использовать линейную регрессию для прогнозирования цены дома, используя 2 характеристики: площадь дома в квадратных метрах и количество спален, пользовательская формула выглядела бы примерно так:
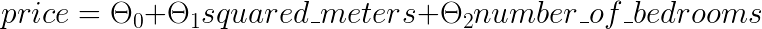
Хорошо, это кажется довольно интуитивно понятным. Теперь, как нам вычислить значения Θi, которые лучше всего подходят к нашим данным? Очень просто: используя наши данные для обучения модели линейной регрессии.
Чтобы убедиться, что мы все находимся в одной точке, наши обучающие данные являются маркированными данными: это данные, содержащие объективное значение, которое мы хотим вычислить для новых точек данных, не имеющих этого значения. В нашем примере с ценой дома обучающие данные состоят из большого количества домов с указанием их цены, площади в квадратных метрах и количества спален.
После обучения модели мы могли бы использовать ее для прогнозирования цены домов по площади в квадратных метрах и количеству спален.
Шаги для обучения модели следующие:
- Во-первых, мы должны выбрать метрику, которая покажет нам, насколько хорошо работает наша модель, сравнивая прогнозы, сделанные моделью для домов в обучающем наборе, с их фактическими ценами. Этими метриками являются такие показатели, как среднеквадратичная ошибка (MSE) или корневая среднеквадратичная ошибка (RMSE).
- Мы устанавливаем параметры модели (Θi) на определенное значение (обычно случайное) и вычисляем эту ошибку для всех обучающих данных.
- Мы итеративно изменяем эти параметры, чтобы минимизировать эту ошибку. Это делается с помощью таких алгоритмов, как градиентный спуск, о котором я сейчас кратко расскажу.
Обучение с помощью градиентного спуска
Градиентный спуск - это алгоритм оптимизации, который может быть использован для решения широкого круга задач. Общая идея этого метода заключается в итеративном изменении параметров модели с целью достижения набора значений параметров, которые минимизируют ошибку, которую делает модель в своих предсказаниях.
После того как параметры модели были инициализированы случайным образом, каждая итерация градиентного спуска проходит следующим образом: при заданных значениях параметров мы используем модель для предсказания каждого экземпляра обучающих данных и сравниваем это предсказание с фактическим значением цели.
Вычислив суммарную ошибку (известную как функция стоимости), мы измеряем локальный градиент этой ошибки по отношению к параметрам модели и обновляем эти параметры, сдвигая их в направлении убывающего градиента, что приводит к уменьшению функции стоимости.
На следующем рисунке графически показано, как это делается: мы начинаем с оранжевой точки, которая является начальным случайным значением параметров модели. После одной итерации градиентного спуска мы переходим к синей точке, которая находится прямо справа и снизу от начальной оранжевой точки: мы движемся в направлении нисходящего градиента.
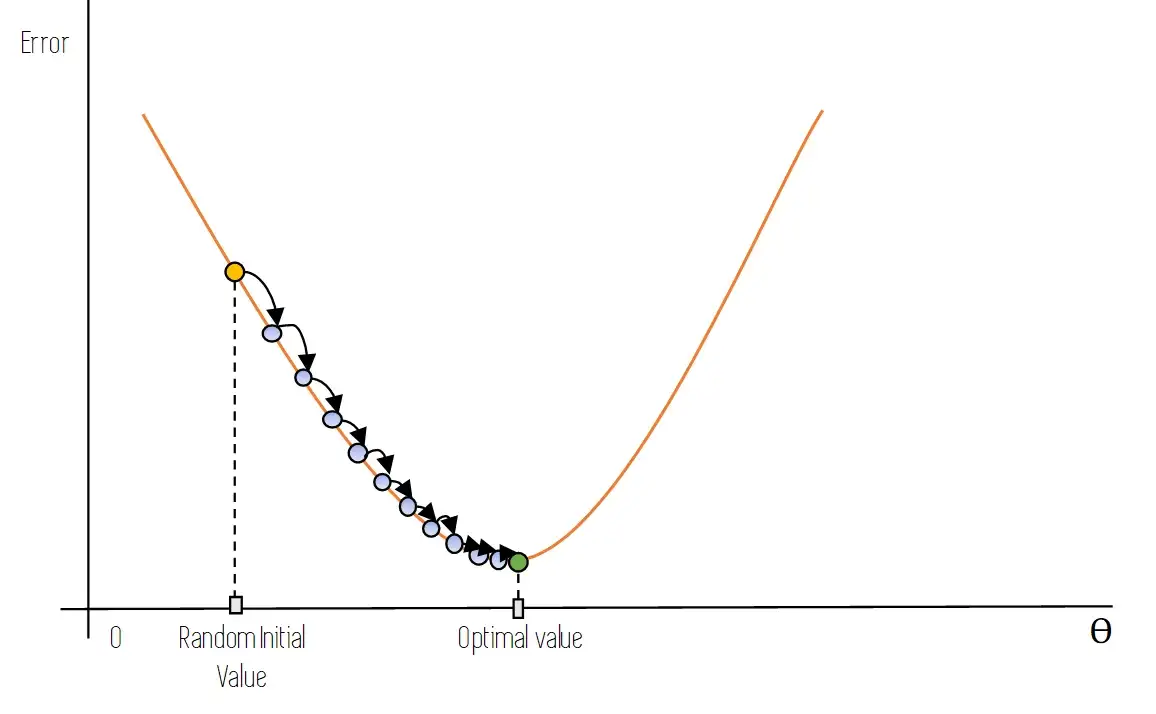
Итерация за итерацией мы движемся вдоль оранжевой кривой ошибок, пока не достигнем оптимального значения, расположенного в нижней части кривой и представленного на рисунке зеленой точкой.
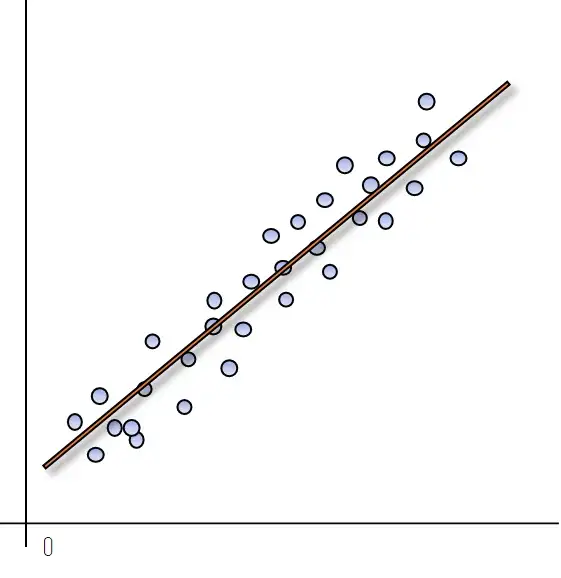
Представьте, что у нас есть линейная модель только с одной характеристикой (x1), чтобы было легче построить график. На следующем рисунке синие точки представляют наши экземпляры данных, для которых у нас есть значение цели (например, цена дома) и значение одной характеристики (например, квадратных метров дома).
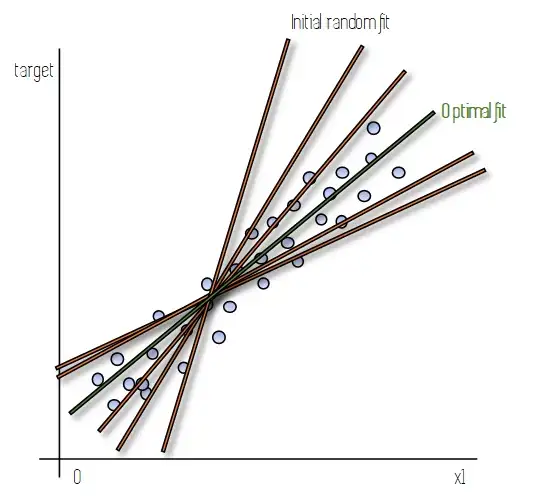
На практике, когда мы обучаем модель с помощью градиентного спуска, происходит то, что мы начинаем с подгонки линии к нашим данным (линия начальной случайной подгонки), которая не очень хорошо их отображает. После каждой итерации градиентного спуска, по мере обновления параметров, эта линия меняет свой наклон и место пересечения с осью y. Этот процесс повторяется, пока мы не достигнем набора значений параметров, которые достаточно хороши (это не всегда оптимальные значения), или пока мы не завершим определенное количество итераций.
Эти параметры представлены зеленой линией оптимального соответствия.
Это легко представить для модели с одним признаком, так как уравнение линейной модели совпадает с уравнением прямой, которое мы изучали в средней школе. Для большего числа признаков применима та же механика, однако ее не так легко визуализировать.
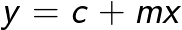
После того как мы завершили процесс и смогли обучить нашу модель с помощью этой процедуры, мы можем использовать ее для новых прогнозов! Как показано на следующем рисунке, используя нашу линию оптимального соответствия и зная квадратные метры дома, мы можем использовать эту линию для прогнозирования того, сколько он будет стоить.
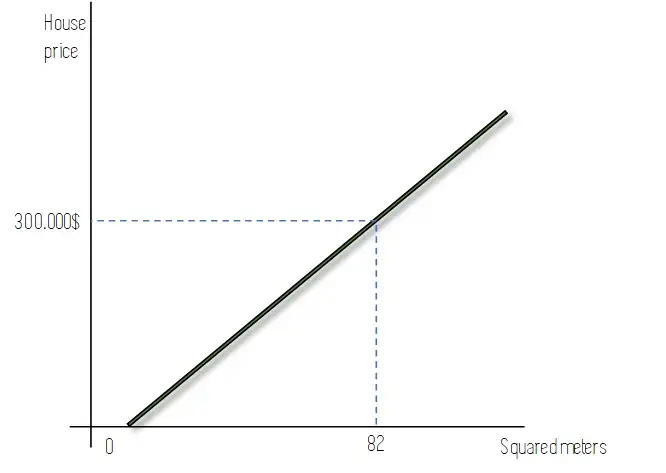
Конечно, это была бы очень простая модель, и, вероятно, не очень точная, поскольку существует множество факторов, влияющих на цену дома. Однако если мы увеличим количество релевантных характеристик, линейная регрессия может дать нам довольно хорошие результаты для простых задач.
Заключение и другие ресурсы
Линейная регрессия - одна из самых простых моделей машинного обучения. Такие модели легко понять, интерпретировать, и они могут давать довольно хорошие результаты. Целью этой статьи было дать простой способ понять линейную регрессию в нематематической манере для людей, которые не являются практиками Machine Learning, поэтому если вы хотите углубиться или ищете более глубокие математические объяснения, посмотрите следующее видео, в нем очень хорошо объясняется все, о чем мы говорили в этой статье.
Вот и все, надеюсь, вам понравилась эта статья. Не стесняйтесь подписываться на наш телеграмм канал @nerditru.
Приятного чтения!
Информация, изложенная здесь, была взята из книги, а также из некоторых других ресурсов.

