Объяснение метода опорных векторов (SVM)
Узнайте всё о методе опорных векторов (SVM)
В этом посте мы раскроем всю магию того, что происходит в SVM, расскажем немного об истории и проясним, когда этот метод следует и не следует использовать.
Мы пройдемся по теории SVM, рассмотрим минимальное количество математики, необходимое для понимания того, как все работает, не погружаясь в детали.
Приступим к делу!

Введение
Метод опорных векторов или SVM - это широко используемое семейство моделей машинного обучения, которые могут решать множество задач машинного обучения, таких как линейная или нелинейная классификация, регрессия или даже обнаружение аномалий.
Тем не менее, наилучшее применение они находят при классификации небольших или средних по размеру сложных наборов данных. На протяжении этой статьи станет ясно, почему.
Чтобы понять, как работают SVM, лучше всего сначала изучить линейные SVM, жесткую и мягкую классификацию.
Линейная SVM-классификация
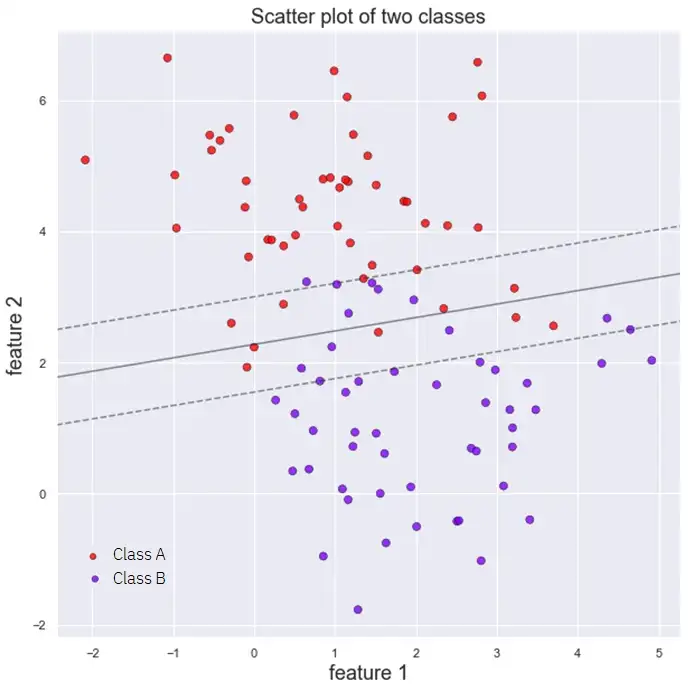
Представьте, что у нас есть следующий набор данных, содержащий всего две характеристики (характеристика 1 и характеристика 2), представляющие два различных класса (класс A и класс B).
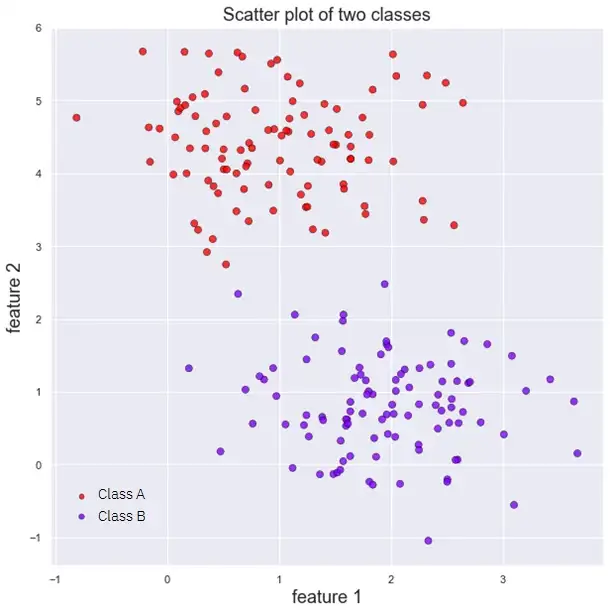
Обычный линейный классификатор попытался бы провести линию, которая идеально разделяет оба класса наших данных. Однако, как видно из следующего рисунка, существует множество линий, которые могут это сделать. Какую из них мы должны выбрать?
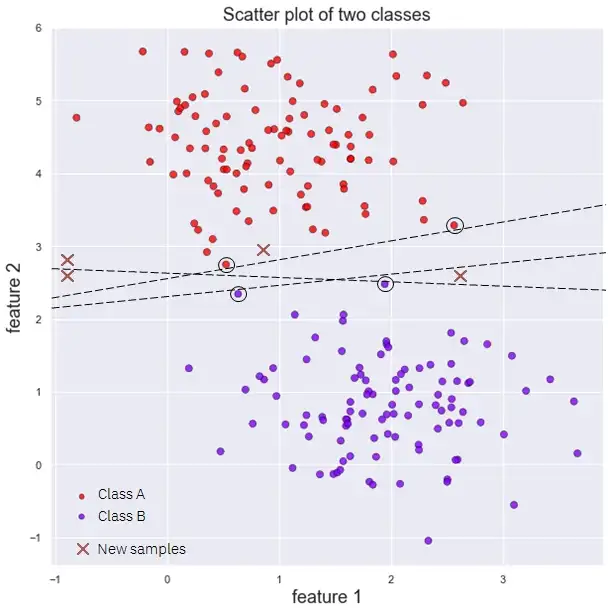
Предыдущие границы принятия решений разделяют обучающие данные с абсолютным совершенством, однако они настолько близко подходят к обучающим экземплярам (красные и фиолетовые точки с черным кругом вокруг них), что, вероятно, они будут очень плохо обобщать новые данные (New samples на рисунке).
Классификаторы с жесткой и мягкой границей
Метод опорных векторов пытается решить эту проблему путем подгонки линии к модели, которая стремится максимизировать расстояние до ближайших обучающих экземпляров (известных как опорные векторы), так чтобы поле, параллельное линии границы принятия решения, было как можно шире.
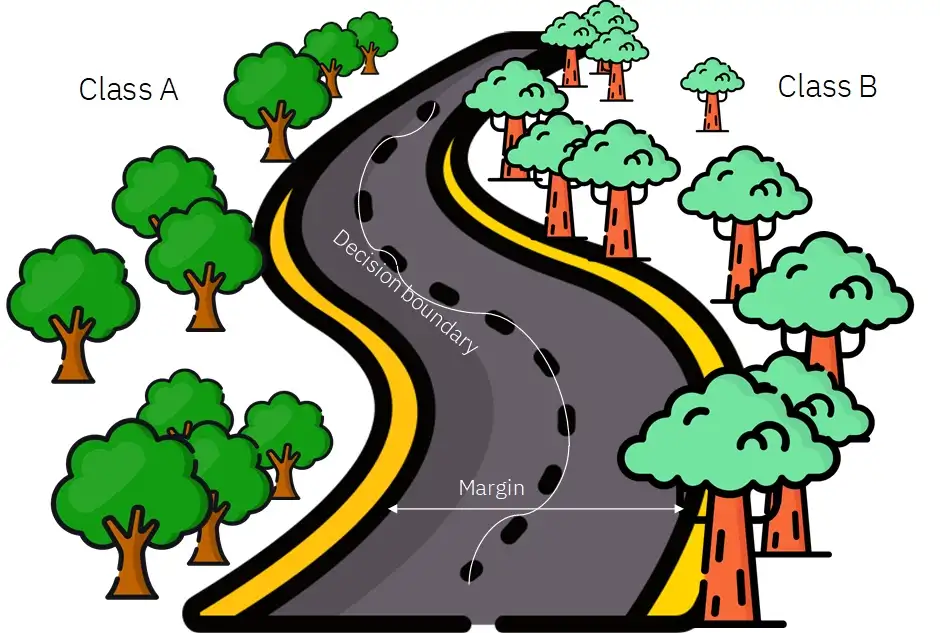
Представьте себе границу принятия решения как центр проселочной дороги, а данные - как деревья, причем деревья разных типов находятся на каждой стороне дороги. SVM пытается найти как можно более широкую дорогу, разделяющую два вида деревьев, чтобы мы могли спокойно проехать по ней, чувствуя себя в безопасности. Для этого она пытается максимизировать границы.
Если теперь рассмотреть предыдущий набор данных, подогнать к нему линейный классификатор опорных векторов (Linear Support Vector Classifier, Linear SVC) и построить границу принятия решения с запасом, то мы получим следующий рисунок:
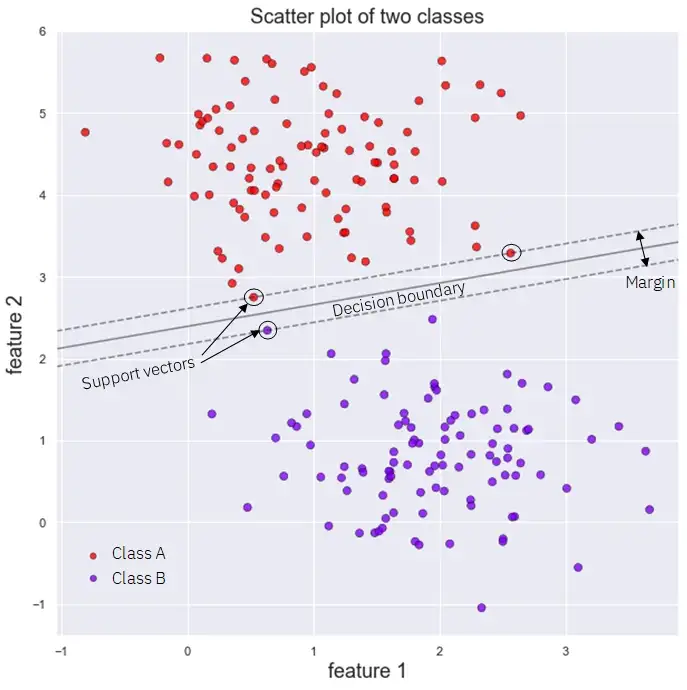
В этом типе SVC ни одной точке не разрешается пересекать границу: мы говорим о классификаторе с жесткой границей. Когда некоторым точкам разрешено пересекать линию поля, что позволяет нам вписать более широкую улицу, мы говорим о классификаторе мягких границ.
Интересно отметить, что для классификатора с жесткой границей соответствие зависит только от положения опорных векторов: добавление точек к нашим обучающим данным, которые не касаются улицы (но находятся на правильной стороне), оставит границу принятия решения и границу нетронутыми.
Граница полностью определяется или "поддерживается" этими ключевыми точками опорного вектора, что и дало им и алгоритму их название. Однако классификаторы с жесткой границей работают только тогда, когда данные идеально разделимы линейным образом, а также очень чувствительны к аномалиям.
Чтобы решить эту проблему, мы переходим к классификаторам с мягкой границей, которые представляют собой более гибкие модели, позволяющие некоторым точкам пересекать границу, что приводит нас к компромиссу между шириной улицы и количеством нарушений границы (точек, находящихся внутри улицы или по ту сторону границы принятия решения). На следующем рисунке показан линейный классификатор с мягкой границей
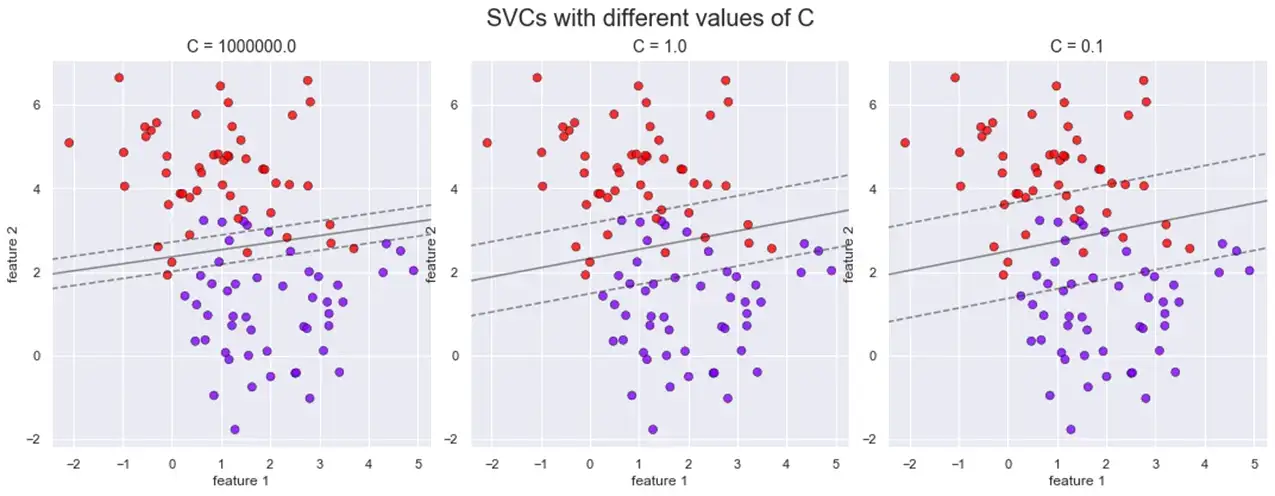
В большинстве реализаций SVC мы контролируем это с помощью гиперпараметра модели (C в Scikit-Learn). Более низкое значение этого параметра означает, что мы имеем более широкую границу с большим количеством нарушений границ, что приводит к более гибкой модели, которая лучше обобщает. Уменьшая C, мы можем регуляризировать нашу модель, если нам кажется, что она слишком хорошо подходит.
Увеличение значения C приводит нас к классификаторам с жесткой границей. На следующем рисунке показано такое поведение: при уменьшении значения C улица становится шире, но у нас больше точек, которые ее пересекают.
Нелинейные SVM-классификаторы
В большинстве случаев, однако, наборы данных не являются линейно разделяемыми, и смягчение нашего поля не совсем помогает.
Один из способов превратить нелинейно разделяемый набор данных в разделяемый - включить дополнительные признаки, полученные из исходных, например, с помощью полиномиальных признаков или методов признаков подобия, таких как радиальные базисные функции (RBF).
На следующем рисунке показано, как путем преобразования набора данных с одним признаком в набор данных с двумя признаками с помощью полинома второй степени мы можем линейно разделить два существующих класса.
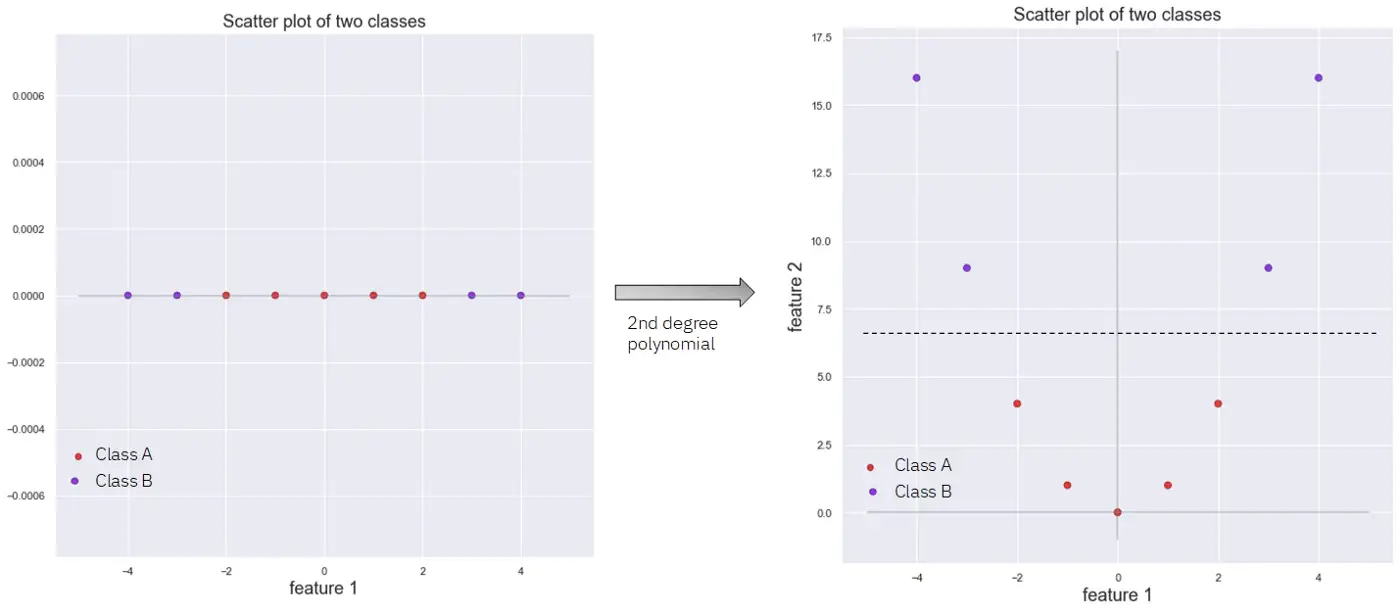
Проблема здесь заключается в том, что с увеличением числа признаков вычислительные затраты на вычисление полиномиальных признаков высокой степени резко возрастают, что делает модель медленной.
Другим способом сделать набор данных линейно разделяемым являются радиальные базисные функции, упомянутые ранее. Следующий пример показывает, как мы можем преобразовать нелинейно разделяемый набор данных в такой, который можно легко разделить с помощью RBF:
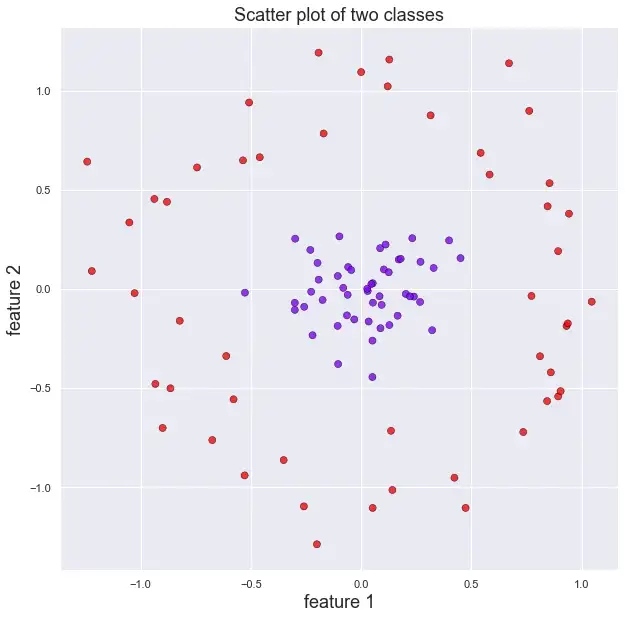
Теперь, если на наборе данных, показанном на предыдущем рисунке, вычислить третью особенность, используя RBF с центром в начале координат, и построить эту новую особенность вместе с двумя предыдущими, наш набор данных преобразуется в следующий, который можно линейно разделить горизонтальной плоскостью на высоте 0,7 по новой характеристике r.
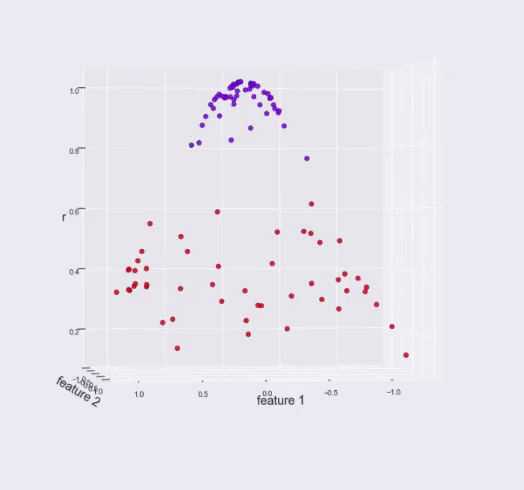
Однако в предыдущем примере мы выбрали точку для центра нашей RBF, которая дала нам хорошие результаты, что нетривиально сделать в большинстве случаев. В большинстве случаев вычисляется RBF от каждой точки в наборе данных до всех других точек данных с использованием исходных характеристик, и эти вычисленные RBF расстояния используются в качестве новых характеристик.
Проблема здесь в том, что если у нас большой обучающий набор, то вычисление всех этих характеристик требует больших вычислительных затрат. И снова мы сталкиваемся с проблемами, когда пытаемся использовать линейный SVC для разделения нелинейных данных.
В решении этих проблем и заключается истинная сила метода опорных векторов: Ядра.
Трюк с ядром
В обоих предыдущих случаях, чтобы разделить наши данные, нам нужно было вычислить преобразования (полиномиальное преобразование и функцию подобия RBF), что, как мы видели, требует больших вычислительных затрат.
Ядро в машинном обучении - это математическая функция, которая позволяет нам вычислить точечное произведение преобразований двух векторов без необходимости вычислять сами преобразования.
Идея ядра иллюстрируется следующей формулой.
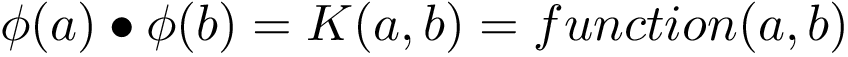
K(a,b) в предыдущей формуле представляет собой ядро векторов a и b (случайное ядро, позже мы увидим, что существует множество различных ядер). Мы видим, что это ядро равно точечному произведению ϕ(a) и ϕ(b), где ϕ представляет собой определенное преобразование (которое может быть полиномом или RBF-преобразованием) вектора, который дается ему в качестве аргумента.
Чтобы понять, как это значительно упрощает нашу задачу, и как с помощью ядер мы можем использовать SVM для классификации нелинейно разделяемых наборов данных, лучше всего сначала посмотреть, как обучается машина опорных векторов.
Обучение SVM: Еще одна оптимизационная задача
В конечном итоге обучение SVM-классификатора сводится к решению оптимизационной задачи, называемой двойной задачей. SVM делает предсказания практически так же, как и любой другой классификатор: он берет входной вектор x, умножает его на некоторый весовой вектор w и добавляет член смещения b, как показано в следующей формуле.
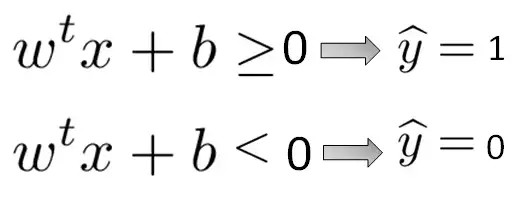
Если эта операция дает результат, превышающий некоторый порог (в нашем случае 0), то образец классифицируется как положительный (1). Если результат меньше порога, то образец классифицируется как отрицательный (0).
Чтобы получить векторы веса и смещения, мы должны решить оптимизационную задачу, которая пытается максимизировать границы улицы, о которой мы говорили, ограничивая при этом нарушения границ. Математически это выражается в нахождении минимального значения весового вектора, который удовлетворяет определенному условию нечеткости или слабины (сколько раз и насколько сильно может быть пересечена граница).
Эта оптимизационная задача может быть решена с помощью обычного QP-решателя, поскольку это выпуклая квадратичная задача. Конечное уравнение, которое решает эта задача, следующее:
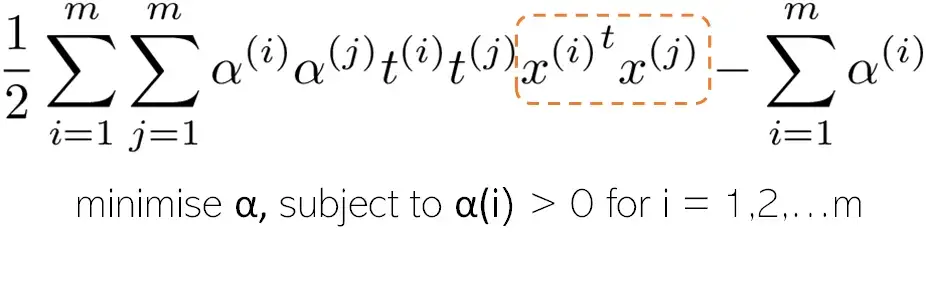
Формула 3, однако, не совсем верна. α должно быть больше или равно 0, принимая это последнее значение для каждой точки данных, которая не является опорным вектором.
Не обращайте внимания на t(i) или t(j), в этом уравнении есть два важных момента: решив его и получив значение α, мы можем рассчитать векторы веса и смещения. Другая вещь, на которую следует обратить внимание, - это член уравнения внутри оранжевой пунктирной линии: точечное произведение двух обучающих экземпляров, которое мы должны повторить для всего обучающего множества.
Именно здесь пригодится трюк с ядром, о котором мы говорили ранее: если бы мы преобразовали наши учебные экземпляры, чтобы сделать их разделяемыми с помощью какого-либо преобразования, нам пришлось бы вычислять преобразование для каждого учебного экземпляра, выполнять точечное произведение... и все это было бы невероятно дорого с точки зрения вычислений. Это показано в следующей формуле.
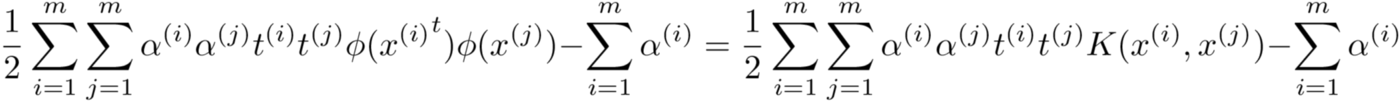
Если, как описано выше, мы используем ядро, то нам не нужно вычислять преобразования. Круто, правда? Давайте посмотрим на некоторые из самых популярных ядер:
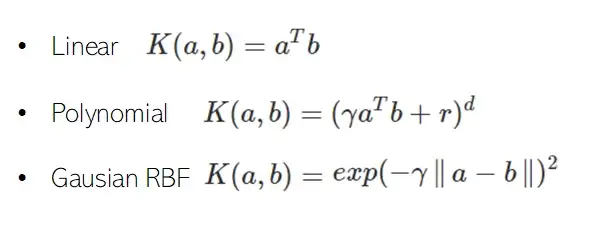
Обратите внимание, что для точечного произведения двух векторов, к которым мы применяем полиномиальное преобразование степени d, где мы теоретически увеличиваем число признаков наших данных и, следовательно, сложность, мы можем использовать ядро, чтобы избежать вычисления этого преобразования и просто вычислить (γaTb+r)d.
В этом и заключается волшебство SVM. Мы можем обучать их и делать прогнозы, получая преимущества выполнения операций над нашими данными без необходимости вычислять эти операции.
Теперь давайте уже подведем итоги, чтобы увидеть красоту того, как на самом деле делаются эти предсказания.
Составление прогнозов с помощью SVM: Опорные векторы
Как мы видели ранее, чтобы сделать прогноз, мы должны вычислить точечное произведение нашего весового вектора и нашей новой точки данных x(n) и добавить член смещения. Для этого, если мы подставим в уравнение формулы 2 значение w, полученное в результате решения задачи оптимизации, мы получим:
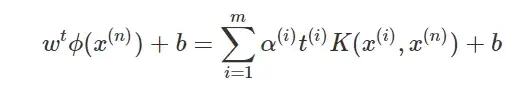
Помните, мы говорили, что α равно 0 для всех точек данных, которые не являются опорными векторами? Это означает, что для прогнозирования нам нужно просто вычислить ядро векторов поддержки и наших новых точек данных и добавить член смещения. Здорово, правда?
Ядра и SVM снова демонстрируют свою магию. И наконец, вот несколько практических советов и рекомендаций по использованию метода опорных векторов.
Дополнительные советы и рекомендации:
- Стандартизация или нормализация данных перед установкой SVM. Перед обучением SVM важно применить какой-либо метод масштабирования. Если наши признаки имеют очень разные масштабы, наши "улицы" будут выглядеть довольно странно, и наши алгоритмы будут работать плохо.
- Как правило, при настройке SVM сначала используйте линейное ядро, особенно если обучающий набор очень большой или в нем большое количество признаков. Если результаты вас не удовлетворяют, попробуйте использовать RBF-ядро; как правило, оно работает довольно хорошо. Затем, если у вас мало времени и вычислительных мощностей, попробуйте другой вид ядер с перекрестной валидацией.
- SVM также можно использовать для регрессии и обнаружения аномалий.
- Однако наилучшие результаты достигаются при использовании их для задач классификации на сложных, но небольших наборах данных.
Заключение
Вот и все! Мы изучили суть метода SVM и некоторые математические принципы его работы.
Вот и все, надеюсь, вам понравилась эта статья. Не стесняйтесь подписываться на наш телеграмм канал @nerditru.
Берегите себя и наслаждайтесь искусственным интеллектом!
Спасибо за чтение!

