Объяснение деревьев принятия решений
Узнайте все о Деревьях решений для машинного обучения
В этой статье я объясню деревья принятия решений простыми словами. Это можно считать статьей "Деревья принятия решений для чайников", но мне никогда не нравилось это выражение.

Прежде чем мы начнем, вот несколько дополнительных ресурсов, которые помогут вам взлететь по карьерной лестнице в Machine Learning.
Введение
В мире машинного обучения деревья решений - это разновидность непараметрических моделей, которые могут использоваться как для классификации, так и для регрессии.
Это означает, что деревья решений - гибкие модели, которые не увеличивают количество параметров по мере добавления новых признаков (если мы правильно их строим), и они могут выдавать либо предсказание по категориям (например, является ли растение определенным видом или нет), либо числовое предсказание (например, цена дома).
Они строятся с помощью двух видов элементов: узлов и ветвей. В каждом узле оценивается одна из характеристик наших данных, чтобы разделить наблюдения в процессе обучения или заставить конкретную точку данных следовать определенному пути при составлении прогноза.
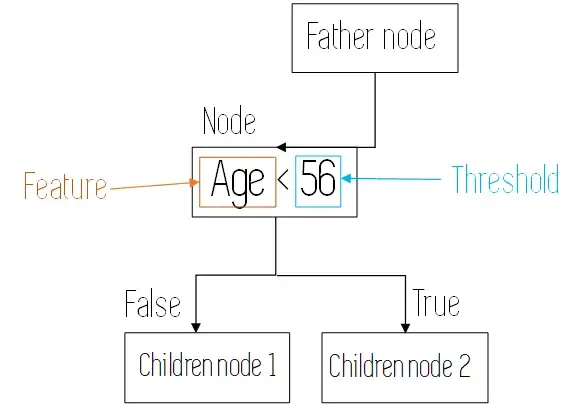
При их построении деревья решений строятся путем рекурсивного оценивания различных признаков и использования в каждом узле признака, который наилучшим образом разделяет данные. Это будет подробно объяснено позже.
Вероятно, лучший способ начать объяснение - посмотреть, как выглядит дерево решений, чтобы быстро сформировать интуитивное представление о том, как их можно использовать. На следующем рисунке показана общая структура одного из таких деревьев.
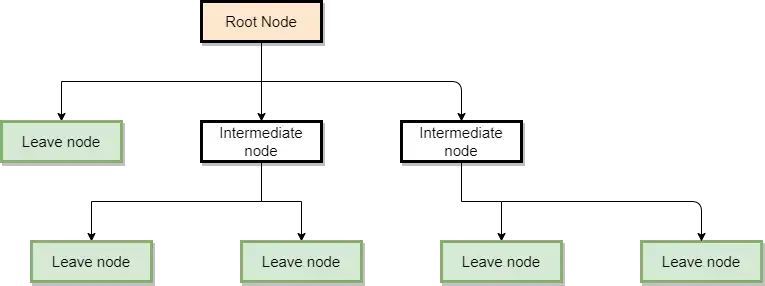
На этом рисунке мы можем наблюдать три вида узлов:
- Корневой узел: Это узел, с которого начинается граф. В обычном дереве решений он оценивает переменную, которая наилучшим образом разделяет данные.
- Промежуточные узлы: Это узлы, в которых оцениваются переменные, но которые не являются конечными узлами, где делаются прогнозы.
- Листовые узлы: Это конечные узлы дерева, в которых делаются предсказания категории или числового значения
И так, с этим разобрались. Теперь, когда у нас есть общее представление о том, что такое деревья принятия решений, давайте посмотрим, каким образом они строятся.
Процесс обучения дерева решений
Как мы уже говорили, деревья решений строятся путем рекурсивного разбиения наших обучающих выборок с использованием тех характеристик данных, которые лучше всего подходят для конкретной задачи. Это делается путем оценки определенных показателей, таких как индекс Джини или энтропия для категориальных деревьев решений, остаточная или средняя квадратичная ошибка для деревьев регрессии.
Процесс также отличается, если признак, который мы оцениваем в узле, является дискретным или непрерывным. Для дискретных признаков оцениваются все их возможные значения, в результате чего для каждой из переменных вычисляется N метрик, причем N - это количество возможных значений для каждого категориального признака. Для непрерывных признаков в качестве возможных порогов используется среднее значение каждых двух последовательных значений (упорядоченных от наименьшего к наибольшему) обучающих данных.
Результатом этого процесса для определенного узла является список переменных, каждая с различными порогами, и рассчитанная метрика (Gini или MSE) для каждого тандема переменная/порог. Затем мы выбираем комбинацию переменных/порогов, которая дает нам наибольшее/меньшее значение для конкретной метрики, которую мы используем для результирующих дочерних узлов (наибольшее уменьшение или увеличение метрики).
Мы не будем углубляться в то, как рассчитываются эти метрики, поскольку это не является темой данного вводного сообщения, однако я оставлю несколько ресурсов в конце, чтобы вы могли углубиться, если вам это интересно. На данный момент просто представьте эти метрики (Gini для категориальных деревьев и Mean Squared Error для деревьев регрессии) как некую ошибку, которую мы хотим уменьшить.
Давайте рассмотрим пример двух деревьев решений, категориального и регрессионного, чтобы получить более четкое представление об этом процессе. На следующем рисунке показано категориальное дерево, построенное для известного набора данных Iris Dataset, где мы пытаемся предсказать категорию из трех различных цветов, используя такие характеристики, как ширина и длина лепестка, длина чашелистика, ...
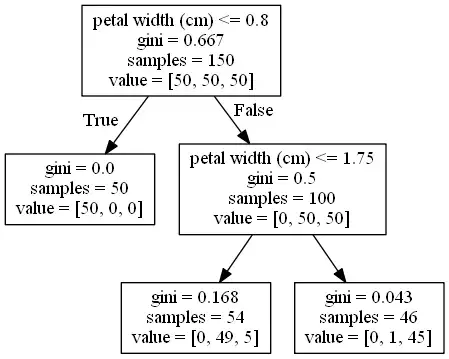
Мы видим, что корневой узел начинается с 50 образцов каждого из трех классов, а индекс Джини (поскольку это категориальное дерево, чем ниже индекс Джини, тем лучше) составляет 0,667.
В этом узле признаком, который наилучшим образом разделяет различные классы данных, является ширина лепестка в см, используя в качестве порога значение 0,8. В результате получаются два узла, один с Gini 0 (абсолютно чистый узел, в котором присутствует только один из типов цветов) и один с Gini 0,5, в котором сгруппированы два других типа цветов.
В этом промежуточном узле (Ложный путь от корневого узла) оценивается тот же признак (да, такое может случиться, и это действительно часто происходит, если признак важен) с использованием порога 1,75. Теперь это приводит к двум другим дочерним узлам, которые не являются чистыми, но имеют довольно низкий индекс Джини.
Во всех этих узлах все остальные признаки данных (длина чашелистика, ширина чашелистика и длина лепестка) были оценены и рассчитан их результирующий индекс Джини, однако признаком, который дал нам наилучшие результаты (самый низкий индекс Джини), оказалась ширина лепестка.
Причина, по которой дерево не продолжало расти, заключается в том, что деревья решений всегда имеют условия остановки роста, иначе они будут расти до тех пор, пока каждая обучающая выборка не будет выделена в отдельный листовой узел. Этими условиями остановки являются максимальная глубина дерева, минимальное количество образцов в узлах листьев или минимальное уменьшение метрики ошибки.
Давайте теперь проверим дерево регрессии, для этого мы будем использовать набор данных по ценам на жилье в Бостоне, в результате чего получим следующий график:

Как видно из предыдущего рисунка, теперь у нас не индекс Джини, а MSE (средняя квадратичная ошибка). Как и в предыдущем примере с Джини, наше дерево построено с использованием комбинаций признаков/порогов, которые в наибольшей степени уменьшили эту ошибку.
В корневом узле используется переменная LSTAT (% низшего статуса населения в районе) с порогом 9,725, чтобы первоначально разделить выборки. Мы видим, что в корневом узле у нас есть 506, которые мы разделили на 212 (левый дочерний узел) и 294 (правый дочерний узел).
В левом дочернем узле используется переменная RM (количество комнат на жилище) с порогом 6,631, а в правом узле - та же переменная LSTAT с порогом 16,085, в результате чего получаются четыре прекрасных листовых узла. Как и раньше, все остальные переменные оценивались в каждом узле, но именно эти две наилучшим образом разделили данные.
Потрясающе! Теперь мы знаем, как строятся деревья решений. Давайте узнаем, как они используются для прогнозирования.
Составление прогнозов с помощью дерева решений
Предсказать категорию или числовое целевое значение нового образца очень просто с помощью Деревьев решений. Это одно из главных преимуществ таких алгоритмов. Все, что нам нужно сделать, это начать с корневого узла, посмотреть на значение признака, который он оценивает, и в зависимости от этого значения перейти к левому или правому дочернему узлу.
Этот процесс повторяется до тех пор, пока мы не достигнем листового узла. Когда это происходит, в зависимости от того, сталкиваемся ли мы с проблемой классификации или регрессии, могут произойти две вещи:
a) Если мы сталкиваемся с проблемой классификации, то прогнозируемой категорией будет способ категорий на этом узле листа. Помните, как в дереве классификации у нас было значение = [0,49,5] в узле среднего листа? Это означает, что тестовая выборка, которая достигает этого узла, имеет наибольшую вероятность принадлежности к классу с 49 обучающими выборками на этом узле, поэтому мы классифицируем ее как таковую.
б) Для дерева регрессии предсказание, которое мы делаем в конце, является средним значением значений целевой переменной в узле листа. В нашем примере с жильем, если в узле листьев было 4 образца с ценами 20, 18, 22 и 24, то прогнозируемое значение в этом узле будет 21, среднее значение из 4 учебных примеров, которые заканчиваются в этом узле.
На следующем рисунке показано, как будет делаться предсказание для нового тестового образца (дом) для предыдущего дерева регрессии.
Примечание: показаны только те признаки дома, которые используются в дереве.

Отлично! Теперь мы знаем, как делать прогнозы с помощью деревьев решений. Давайте закончим изучение их преимуществ и недостатков.
Плюсы и минусы деревьев решений
Преимущества:
- Основное преимущество деревьев решений заключается в том, насколько легко их интерпретировать. В то время как другие модели машинного обучения близки к черным ящикам, деревья решений предоставляют графический и интуитивный способ понять, что делает наш алгоритм.
- По сравнению с другими алгоритмами машинного обучения деревья решений требуют меньше данных для обучения.
- Их можно использовать для классификации и регрессии.
- Они просты.
- Они терпимы к отсутствующим значениям.
Недостатки
- Они склонны к чрезмерной подгонке обучающих данных и могут быть чувствительны к выбросам.
- Они слабо обучаемы: одиночное дерево решений обычно не дает хороших прогнозов, поэтому несколько деревьев часто объединяют в "леса" для создания более сильных ансамблевых моделей. Об этом будет рассказано в следующей статье.
Заключение и дополнительные ресурсы
Деревья решений - это простые, но интуитивно понятные алгоритмы, и поэтому они часто используются при попытке объяснить результаты модели машинного обучения. Несмотря на свою слабость, они могут быть объединены в модели bagging или boosting, которые являются очень мощными. В следующих заметках мы рассмотрим некоторые из этих моделей.
Если вы хотите узнать полный процесс построения дерева, посмотрите следующее видео:
Вот и все, надеюсь, вам понравилась эта статья. Не стесняйтесь подписываться на наш телеграмм канал @nerditru.
Большое спасибо, что прочитали, и хорошего дня!

