Прогнозирование временных рядов: анализ и применение методов машинного обучения
Прогнозирование временных рядов является важной задачей в сфере анализа данных и принятия решений. Временные ряды представляют собой последовательность данных, упорядоченных по времени, и включают такие области, как финансовые рынки, погода, продажи и другие.
В данной статье мы рассмотрим основные методы прогнозирования временных рядов с использованием машинного обучения.
Анализ временных рядов
Введение в временные ряды
Объяснение основных понятий и терминов, связанных с временными рядами, таких как тренд, сезонность и шум.
Временные ряды являются важным инструментом анализа данных, используемым для изучения изменений во времени. Они широко применяются в различных областях, таких как экономика, финансы, метеорология, маркетинг и другие. В данной статье мы рассмотрим основные понятия и термины, связанные с временными рядами, включая тренд, сезонность и шум.
- Тренд: Тренд представляет собой долгосрочное изменение во временном ряде. Он может быть восходящим (положительным), нисходящим (отрицательным) или отсутствовать вовсе. Тренд позволяет определить общую тенденцию данных и может быть полезным для прогнозирования будущих значений временного ряда.
- Сезонность: Сезонность отражает периодические колебания во временном ряде, которые повторяются с определенной частотой. Например, продажи игрушек могут иметь сезонные колебания, связанные с праздниками. Сезонность может быть ежегодной, квартальной, месячной или иметь другую периодичность.
- Шум: Шум или случайная компонента представляет собой непредсказуемую и случайную вариацию во временном ряде. Шум может быть вызван случайными факторами, ошибками измерений или другими непредсказуемыми событиями. Шум затрудняет прогнозирование временного ряда и может быть исключен при анализе данных.
Визуализация и исследование временных рядов
Методы визуализации временных рядов включают в себя различные типы графиков, которые помогают анализировать и понимать характеристики временных данных. Один из наиболее распространенных методов - это линейные графики. Вот несколько примеров линейных графиков для визуализации временных рядов:
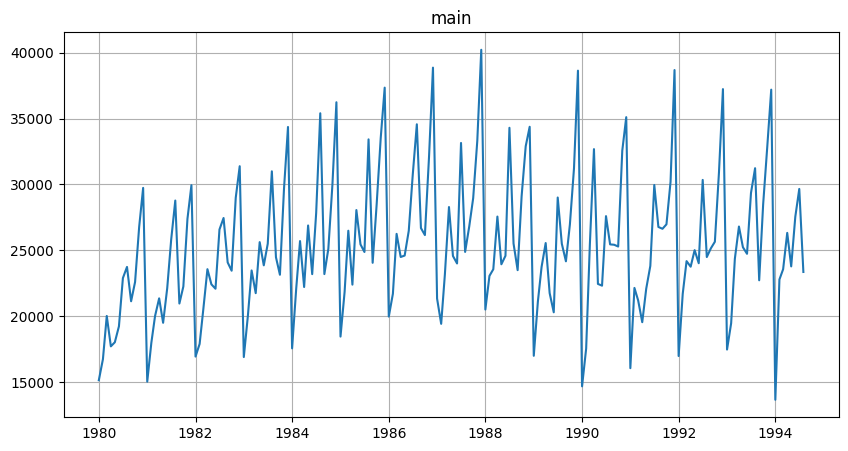
- График временного ряда: Это простой линейный график, где по оси X отображается время, а по оси Y - значения временного ряда. Этот график позволяет наглядно представить изменение значений ряда во времени и выявить тренды, сезонность и выбросы.
- График скользящего среднего: Этот график показывает среднее значение временного ряда на определенном промежутке времени. Он помогает сгладить шумы и выявить общую тенденцию изменения ряда.
- График автокорреляции: Этот график показывает корреляцию между значениями временного ряда и его лагами (отстающими значениями). Он помогает выявить сезонность и другие зависимости в данных.
- График разложения временного ряда: Этот график разделяет временной ряд на его компоненты, такие как тренд, сезонность и остатки. Он позволяет более детально изучить каждую компоненту и выявить особенности ряда.
Примеры кода на Python для визуализации временных рядов с использованием библиотеки pandas:
import pandas as pd
import matplotlib.pyplot as plt
# Загрузка данных временного ряда
data = pd.read_csv("data.csv", parse_dates=True, index_col="Date")
# График временного ряда
plt.plot(data.index, data["Value"])
plt.xlabel("Дата")
plt.ylabel("Значение")
plt.title("График временного ряда")
plt.show()
# График скользящего среднего
rolling_mean = data["Value"].rolling(window=7).mean()
plt.plot(data.index, data["Value"], label="Исходные значения")
plt.plot(data.index, rolling_mean, label="Скользящее среднее")
plt.xlabel("Дата")
plt.ylabel("Значение")
plt.title("График скользящего среднего")
plt.legend()
plt.show()
# График автокорреляции
pd.plotting.autocorrelation_plot(data["Value"])
plt.xlabel("Лаг")
plt.ylabel("Корреляция")
plt.title("График автокорреляции")
plt.show()
# График разложения временного ряда
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(data["Value"], model="additive")
decomposition.plot()
plt.xlabel("Дата")
plt.suptitle("Разложение временного ряда")
plt.show()
Статистические тесты для анализа временных рядов
Тест Дики-Фуллера
Этот тест используется для проверки стационарности временного ряда, то есть постоянства его статистических характеристик во времени.
Пример теста Дики-Фуллера:
Предположим, у нас есть временной ряд данных о ежемесячных продажах товара за последние 5 лет. Мы хотим проверить, является ли этот временной ряд стационарным с помощью теста Дики-Фуллера.
import pandas as pd
from statsmodels.tsa.stattools import adfuller
# Загружаем данные временного ряда
data = pd.read_csv('sales_data.csv')
# Проводим тест Дики-Фуллера
result = adfuller(data['sales'])
# Выводим результаты теста
print('Тестовая статистика: ', result[0])
print('Критические значения: ', result[4])
print('p-значение: ', result[1])В данном примере мы используем библиотеку pandas для загрузки данных временного ряда из файла "sales_data.csv". Затем мы передаем столбец с продажами в функцию adfuller из библиотеки statsmodels, чтобы выполнить тест Дики-Фуллера.
Результаты теста выводятся на экран. Тестовая статистика представляет собой значение, которое сравнивается с критическими значениями для определения статистической значимости. Значение p-значения показывает вероятность того, что нулевая гипотеза о наличии единичного корня верна.
На основе результатов теста Дики-Фуллера можно сделать выводы о стационарности временного ряда. Если тестовая статистика меньше критических значений и p-значение меньше заданного уровня значимости (обычно 0.05), то можно отвергнуть нулевую гипотезу о наличии единичного корня и сделать вывод о стационарности временного ряда.
Тест Льюнга-Бокса
Этот тест используется для проверки автокорреляции значений во временном ряду.
Пример теста Льюнга-Бокса:
Предположим, у нас есть временной ряд данных о ежемесячных температурах за последние 10 лет. Мы хотим проверить наличие автокорреляции в остатках модели с помощью теста Льюнга-Бокса.
import pandas as pd
from statsmodels.stats.diagnostic import acorr_ljungbox
# Загружаем данные временного ряда
data = pd.read_csv('temperature_data.csv')
# Проводим тест Льюнга-Бокса
result = acorr_ljungbox(data['temperature'])
# Выводим результаты теста
print('Тестовая статистика: ', result[0])
print('p-значения: ', result[1])В данном примере мы используем библиотеку pandas для загрузки данных временного ряда из файла "temperature_data.csv". Затем мы передаем столбец с температурами в функцию acorr_ljungbox из библиотеки statsmodels.stats.diagnostic, чтобы выполнить тест Льюнга-Бокса.
Результаты теста выводятся на экран. Тестовая статистика представляет собой значения, которые сравниваются с критическими значениями для определения статистической значимости. Значения p-значений показывают вероятность того, что нулевая гипотеза о отсутствии автокорреляции верна.
На основе результатов теста Льюнга-Бокса можно сделать выводы о наличии автокорреляции в остатках модели. Если значения тестовой статистики меньше критических значений и соответствующие p-значения меньше заданного уровня значимости (обычно 0.05), то можно отвергнуть нулевую гипотезу о отсутствии автокорреляции и сделать вывод о наличии автокорреляции в остатках.
Тест Грейнджера на причинность
Этот тест используется для определения причинно-следственных связей между двумя временными рядами.
Пример теста Грейнджера:
Тест Грейнджера - это статистический тест, который используется для определения причинно-следственной связи между двумя временными рядами. Он позволяет оценить, влияет ли один временной ряд на другой.
Вот пример использования теста Грейнджера для проверки причинно-следственной связи между двумя экономическими временными рядами - ВВП и индексом потребительских цен:
import pandas as pd
from statsmodels.tsa.stattools import grangercausalitytests
# Загружаем данные временных рядов
data = pd.read_csv('economy_data.csv')
# Проводим тест Грейнджера
result = grangercausalitytests(data[['GDP', 'CPI']], maxlag=2)
# Выводим результаты теста
for lag in result.keys():
print(f'Лаг {lag}:')
print('Тестовая статистика: ', result[lag][0]['ssr_ftest'][0])
print('p-значение: ', result[lag][0]['ssr_ftest'][1])
print('---')В данном примере мы используем библиотеку pandas для загрузки данных временных рядов ВВП и индекса потребительских цен из файла "economy_data.csv". Затем мы передаем эти два временных ряда в функцию grangercausalitytests из библиотеки statsmodels.tsa.stattools, чтобы выполнить тест Грейнджера.
Результаты теста выводятся на экран для каждого заданного лага. Тестовая статистика представляет собой значение, которое сравнивается с критическими значениями для определения статистической значимости. Значение p-значения показывает вероятность того, что нулевая гипотеза о отсутствии причинно-следственной связи верна.
На основе результатов теста Грейнджера можно сделать выводы о наличии причинно-следственной связи между временными рядами. Если значение тестовой статистики меньше критических значений и соответствующее p-значение меньше заданного уровня значимости (обычно 0.05), то можно отвергнуть нулевую гипотезу о отсутствии причинно-следственной связи и сделать вывод о наличии такой связи.
Обратите внимание, что в данных примерах мы использовали Python и библиотеку statsmodels для выполнения тестов, но в других языках программирования также доступны аналогичные функции и библиотеки для выполнения этого теста.
Классические методы прогнозирования временных рядов:
Метод скользящего среднего (Moving Average):
Метод скользящего среднего (Moving Average) - это статистический метод, который используется для сглаживания временных рядов путем вычисления среднего значения наблюдений в определенном окне или периоде времени. Он помогает устранить случайные колебания и выявить общие тенденции или паттерны в данных.
Пример использования метода скользящего среднего в Python с использованием библиотеки NumPy:
import numpy as np
# Входные данные
data = [1, 2, 5, 10]
# Вычисление скользящего среднего
n = 2 # Размер окна
moving_average = np.convolve(data, np.ones(n)/n, mode='valid')
# Вывод результатов
print(moving_average)В данном примере мы используем библиотеку NumPy для вычисления скользящего среднего. Входные данные представлены списком data, а переменная n указывает размер окна (количество наблюдений, используемых для вычисления среднего значения). Функция np.convolve применяет скользящее среднее к данным с помощью окна заданного размера. Режим mode='valid' используется для удаления краевых эффектов.
Результаты выводятся на экран и представляют собой список значений скользящего среднего.
Метод скользящего среднего широко используется в анализе временных рядов, финансовой аналитике, прогнозировании и других областях, где требуется сглаживание данных для выявления общих тенденций.
Экспоненциальное сглаживание (Exponential Smoothing):
Экспоненциальное сглаживание (Exponential Smoothing) - это метод анализа временных рядов, который используется для прогнозирования будущих значений на основе предыдущих наблюдений. Он предназначен для сглаживания данных и выявления общих тенденций, учитывая весовые коэффициенты, которые уменьшаются экспоненциально с течением времени.
В экспоненциальном сглаживании каждое новое наблюдение в ряду получает вес, который зависит от предыдущих наблюдений и параметров сглаживания. Более новые наблюдения имеют больший вес, в то время как более старые наблюдения имеют меньший вес. Это позволяет моделировать изменения в данных с учетом последних значений и устранять случайные колебания.
Возможны различные варианты экспоненциального сглаживания, такие как простое экспоненциальное сглаживание (Simple Exponential Smoothing) и двойное экспоненциальное сглаживание (Double Exponential Smoothing). Каждый из них имеет свои особенности и применяется в различных ситуациях.
Вот пример использования экспоненциального сглаживания на Python с использованием библиотеки statsmodels:
import pandas as pd
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
# Входные данные
data = [10, 12, 15, 18, 20, 22, 25, 28, 30]
# Создание модели экспоненциального сглаживания
model = SimpleExpSmoothing(data)
# Обучение модели
model_fit = model.fit()
# Прогнозирование будущих значений
forecast = model_fit.forecast(3) # Прогноз на 3 периода вперед
# Вывод результатов
print(forecast)В данном примере мы используем библиотеку statsmodels для реализации экспоненциального сглаживания. Входные данные представлены списком data, который содержит временной ряд. Мы создаем модель SimpleExpSmoothing и обучаем ее на данных. Затем мы используем метод forecast для прогнозирования будущих значений на указанное количество периодов вперед.
Результаты выводятся на экран и представляют собой прогнозные значения для указанного количества периодов вперед.
Обратите внимание, что в данном примере мы использовали модель простого экспоненциального сглаживания (SimpleExpSmoothing), но в библиотеке statsmodels также доступны другие модели экспоненциального сглаживания, такие как Holt и Holt-Winters.
Модели машинного обучения для прогнозирования временных рядов:
Линейная регрессия:
Линейная регрессия - это статистический метод, который используется для оценки и прогнозирования связи между зависимой переменной и одной или несколькими независимыми переменными. Он представляет собой модель, которая стремится найти линейную зависимость между независимыми переменными (X) и зависимой переменной (Y).
Пример использования линейной регрессии на Python с использованием библиотеки scikit-learn:
import numpy as np
from sklearn.linear_model import LinearRegression
# Входные данные
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # Независимая переменная
Y = np.array([2, 4, 6, 8, 10]) # Зависимая переменная
# Создание модели линейной регрессии
model = LinearRegression()
# Обучение модели
model.fit(X, Y)
# Получение прогноза для новых значений
new_X = np.array([6, 7, 8]).reshape(-1, 1)
predicted_Y = model.predict(new_X)
# Вывод результатов
print(predicted_Y)Входные данные представлены массивами X и Y, где X - независимая переменная, а Y - зависимая переменная. Мы создаем модель LinearRegression и обучаем ее на данных. Затем мы используем метод predict для получения прогнозных значений для новых значений независимой переменной new_X.
Результаты выводятся на экран и представляют собой прогнозные значения для новых значений независимой переменной.
Линейная регрессия широко используется в анализе данных, прогнозировании, машинном обучении и других областях, где требуется моделирование и прогнозирование зависимостей между переменными.
Алгоритмы регрессии на основе деревьев решений:
Алгоритмы регрессии на основе деревьев решений - это методы машинного обучения, которые используют деревья решений для моделирования и прогнозирования зависимости между независимыми и зависимой переменными.
Дерево решений - это структура, которая представляет собой древовидную модель принятия решений, где каждый узел представляет тест на одну из независимых переменных, а каждая ветвь представляет возможный результат этого теста. Листья дерева представляют собой прогнозные значения для зависимой переменной.
Алгоритмы регрессии на основе деревьев решений, такие как CART (Classification and Regression Trees) и Random Forest, используют деревья решений для моделирования непрерывных зависимых переменных. Они строят деревья, учитывая разделение данных на основе различных признаков и выбирая наилучшие разделения, чтобы минимизировать ошибку прогнозирования.
Пример использования алгоритма регрессии на основе деревьев решений на Python с использованием библиотеки scikit-learn:
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error
# Загрузка данных
data = load_boston()
X = data.data
y = data.target
# Разделение данных на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Создание модели дерева решений
model = DecisionTreeRegressor()
# Обучение модели
model.fit(X_train, y_train)
# Прогнозирование на тестовой выборке
y_pred = model.predict(X_test)
# Оценка качества модели
mse = mean_squared_error(y_test, y_pred)
print("Mean Squared Error:", mse)В данном примере мы используем библиотеку scikit-learn для реализации алгоритма регрессии на основе деревьев решений. Мы загружаем набор данных Boston Housing, разделяем его на обучающую и тестовую выборки, создаем модель DecisionTreeRegressor и обучаем ее на обучающей выборке. Затем мы делаем прогноз на тестовой выборке и оцениваем качество модели с помощью среднеквадратичной ошибки (Mean Squared Error).
Обратите внимание, что в данном примере использовался один алгоритм регрессии на основе деревьев решений (DecisionTreeRegressor), но в библиотеке scikit-learn также доступны другие алгоритмы, такие как Random Forest, Gradient Boosting и другие.
Рекуррентные нейронные сети (RNN):
Рекуррентные нейронные сети (RNN) - это тип нейронных сетей, которые обрабатывают последовательности данных, учитывая контекст и зависимости между элементами последовательности. Они имеют способность сохранять информацию о предыдущих состояниях и использовать ее для принятия решений на текущем шаге.
RNN широко используются в областях, где важна последовательность данных, таких как обработка естественного языка (Natural Language Processing, NLP), распознавание речи, машинный перевод и временные ряды.
RNN имеют внутреннюю память, которая позволяет им учитывать предыдущие состояния при обработке текущего входа. Это достигается путем передачи информации от предыдущего шага к текущему шагу. Такая архитектура позволяет RNN улавливать долгосрочные зависимости в данных.
Однако, у простых RNN есть проблема исчезающего градиента, когда градиенты становятся слишком малыми и не способны обновлять веса в начальных слоях сети. Для решения этой проблемы были разработаны модификации RNN, такие как Long Short-Term Memory (LSTM) и Gated Recurrent Unit (GRU), которые имеют механизмы для сохранения и обновления информации внутри сети.
Пример использования RNN на основе библиотеки Keras в Python:
from keras.models import Sequential
from keras.layers import Dense, LSTM
# Создание модели RNN
model = Sequential()
model.add(LSTM(64, input_shape=(timesteps, input_dim)))
model.add(Dense(1))
# Компиляция модели
model.compile(loss='mean_squared_error', optimizer='adam')
# Обучение модели
model.fit(X_train, y_train, epochs=10, batch_size=32)
# Прогнозирование на тестовой выборке
y_pred = model.predict(X_test)В данном примере мы используем библиотеку Keras для создания и обучения модели RNN. Мы добавляем слой LSTM с 64 нейронами и указываем форму входных данных. Затем мы добавляем полносвязный слой и компилируем модель с функцией потерь и оптимизатором. После этого мы обучаем модель на обучающей выборке и делаем прогноз на тестовой выборке.
Обратите внимание, что в примере использовался слой LSTM, но в Keras также доступны другие типы RNN, такие как GRU. Конкретная архитектура RNN может быть настроена в зависимости от задачи и данных.
Оценка и выбор модели
Метрики оценки прогнозов:
При оценке прогнозов важно использовать различные метрики, которые позволяют измерить качество модели. Вот некоторые распространенные метрики оценки прогнозов:
- Среднеквадратичная ошибка (Mean Squared Error, MSE): Это одна из наиболее распространенных метрик для оценки точности прогнозов. Она измеряет среднеквадратичное отклонение между прогнозами и фактическими значениями. Чем меньше значение MSE, тем лучше модель. Формула для вычисления MSE: MSE = (1/n) * Σ(y_pred - y_true)^2, где y_pred - прогнозные значения, y_true - фактические значения, n - количество наблюдений.
- Средняя абсолютная ошибка (Mean Absolute Error, MAE): Эта метрика также измеряет отклонение между прогнозами и фактическими значениями, но без возведения в квадрат. Она является более устойчивой к выбросам, чем MSE. Формула для вычисления MAE: MAE = (1/n) * Σ|y_pred - y_true|.
- Коэффициент детерминации (Coefficient of Determination, R^2): Эта метрика измеряет долю дисперсии зависимой переменной, которая объясняется моделью. Значение R^2 находится в диапазоне от 0 до 1, где 1 означает, что модель идеально объясняет вариацию данных, а 0 означает, что модель не объясняет никакой вариации. Формула для вычисления R^2: R^2 = 1 - (SSR/SST), где SSR - сумма квадратов остатков, SST - общая сумма квадратов.
- Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error, MAPE): Эта метрика измеряет процентное отклонение между прогнозами и фактическими значениями. Она полезна, когда важно измерить точность прогнозов в процентном соотношении. Формула для вычисления MAPE: MAPE = (1/n) * Σ(|(y_pred - y_true)/y_true|) * 100.
- Корень среднеквадратичной ошибки (Root Mean Squared Error, RMSE): Эта метрика является квадратным корнем из MSE и измеряет среднеквадратичное отклонение между прогнозами и фактическими значениями. RMSE имеет ту же размерность, что и зависимая переменная, что делает его более интерпретируемым. Формула для вычисления RMSE: RMSE = sqrt(MSE).
Важно выбирать метрики оценки прогнозов, которые наилучшим образом соответствуют конкретной задаче и контексту. Кроме того, можно использовать и другие метрики, в зависимости от требований и особенностей данных.
Выбор модели:
При выборе модели важно учитывать различные факторы, такие как тип задачи, доступные данные и конкретные требования задачи. Вот некоторые общие соображения, которые следует учитывать:
- Тип задачи: Определите тип задачи, которую вы пытаетесь решить. Это задача классификации, задача регрессии или что-то другое? Разные модели разработаны для решения разных типов задач.
- Доступность данных: Оцените доступность и качество ваших данных. Учтите размер набора данных, количество признаков и наличие недостающих или зашумленных данных. Некоторые модели могут требовать больше данных или иметь специфические требования к данным.
- Сложность модели: Учтите сложность модели. Более сложные модели могут иметь большую способность улавливать сложные закономерности в данных, но они также могут быть более подвержены переобучению, особенно при ограниченных данных. Более простые модели могут быть более интерпретируемыми и лучше обобщаться.
- Интерпретируемость: Оцените необходимость интерпретируемости. Некоторые модели, такие как линейная регрессия или деревья решений, предоставляют легко интерпретируемые результаты, что может быть ценным в определенных областях или при объяснении модели заинтересованным сторонам. Другие модели, такие как глубокие нейронные сети, могут обеспечивать более высокую предсказательную эффективность, но могут быть сложными для интерпретации.
- Вычислительные ресурсы: Учтите вычислительные ресурсы, доступные для обучения и развертывания модели. Некоторые модели, например, модели глубокого обучения с большим количеством слоев, могут требовать значительных вычислительных мощностей и времени для обучения.
- Базовая производительность: Определите базовую производительность с помощью простых моделей или эвристик. Это позволит вам оценить улучшение, достигнутое более сложными моделями, и определить, оправдана ли дополнительная сложность.
Важно отметить, что выбор модели часто является результатом итерационного процесса, где вы экспериментируете с различными моделями, оцениваете их производительность и уточняете подход на основе результатов. Рекомендуется начинать с более простых моделей и постепенно увеличивать сложность при необходимости.
Помните, что выбор модели зависит от конкретной задачи и контекста, и всегда полезно экспериментировать и сравнивать различные модели, чтобы найти лучшую подходящую для вашей задачи.

