Объяснение метода случайного леса
О методе случайного леса простыми словами
В этой статье мы объясним, что такое метод случайного леса, рассмотрим его сильные стороны, как он строится и для чего его можно использовать.
Мы пройдемся по теории и метода случайного леса, рассмотрим минимальное количество математики, необходимое для понимания того, как все работает, не погружаясь в самые сложные детали.
И наконец, прежде чем мы начнем, предлагаем вам несколько дополнительных ресурсов, которые помогут вам взлететь по карьерной лестнице в Machine Learning:
Для получения обучающих ресурсов перейдите на сайт Яндекс Практикум!

Введение
В мире машинного обучения модели случайного леса являются разновидностью непараметрических моделей, которые могут использоваться как для регрессии, так и для классификации. Это один из самых популярных комплексных методов, относящийся к особой категории Bagging-методов.
Комплексные методы подразумевают использование множества обучающих устройств для повышения производительности каждого из них в отдельности. Эти методы можно охарактеризовать как технику, которая использует группу слабо обучаемых (тех, которые в среднем достигают лишь немного лучших результатов, чем случайная модель) вместе, чтобы создать более сильную, объединенную модель.
В нашем случае метод случайного леса - это группа из множества отдельных деревьев решений. Если вы не знакомы с Деревьями решений, вы можете узнать о них здесь: Объяснение деревьев решений
Одним из основных недостатков деревьев решений является то, что они очень склонны к чрезмерной адаптации: они хорошо работают на обучающих данных, но не так гибко подходят для прогнозирования на невидимых образцах. Хотя для этого существуют обходные пути, например, обрезка деревьев, это снижает их предсказательную силу. В целом это модели со средней погрешностью и высокой дисперсией, но они просты и легко интерпретируются.
Модели случайного леса сочетают в себе простоту деревьев решений с гибкостью и мощностью групповой модели. В лесу деревьев мы забываем о высокой дисперсии конкретного дерева и меньше заботимся о каждом отдельном элементе, поэтому мы можем вырастить более красивые, большие деревья, которые обладают большей предсказательной силой, чем обрезанные.
Хотя модели Random Forest не обладают такой же способностью к интерпретации, как отдельные деревья, их производительность намного выше, и нам не нужно так сильно беспокоиться об идеальной настройке параметров леса, как в случае с отдельными деревьями.
Окей, случайный лес - это набор отдельных деревьев. Но почему название "Случайный"? Где здесь случайность? Давайте узнаем, как строится модель случайного леса.
Обучение и построение случайного леса
Построение случайного леса состоит из 3 основных этапов. Мы разберем каждый из них и разъясним все понятия и шаги. Поехали!
Создание загрузочного набора данных для каждого дерева
Когда мы строим индивидуальное дерево решений, мы используем набор обучающих данных и все наблюдения. Это означает, что если мы не будем осторожны, дерево может очень хорошо приспособиться к этим обучающим данным и плохо обобщать новые, невидимые наблюдения. Чтобы решить эту проблему, мы не даем дереву вырасти очень большим, обычно ценой снижения его производительности.
Чтобы построить случайный лес, мы должны обучить N деревьев решений. Обучаем ли мы деревья, используя все время одни и те же данные? Используем ли мы весь набор данных? Нет.
Вот здесь и появляется первая случайная особенность. Для обучения каждого отдельного дерева мы выбираем случайную выборку из всего набора данных, как показано на следующем рисунке.
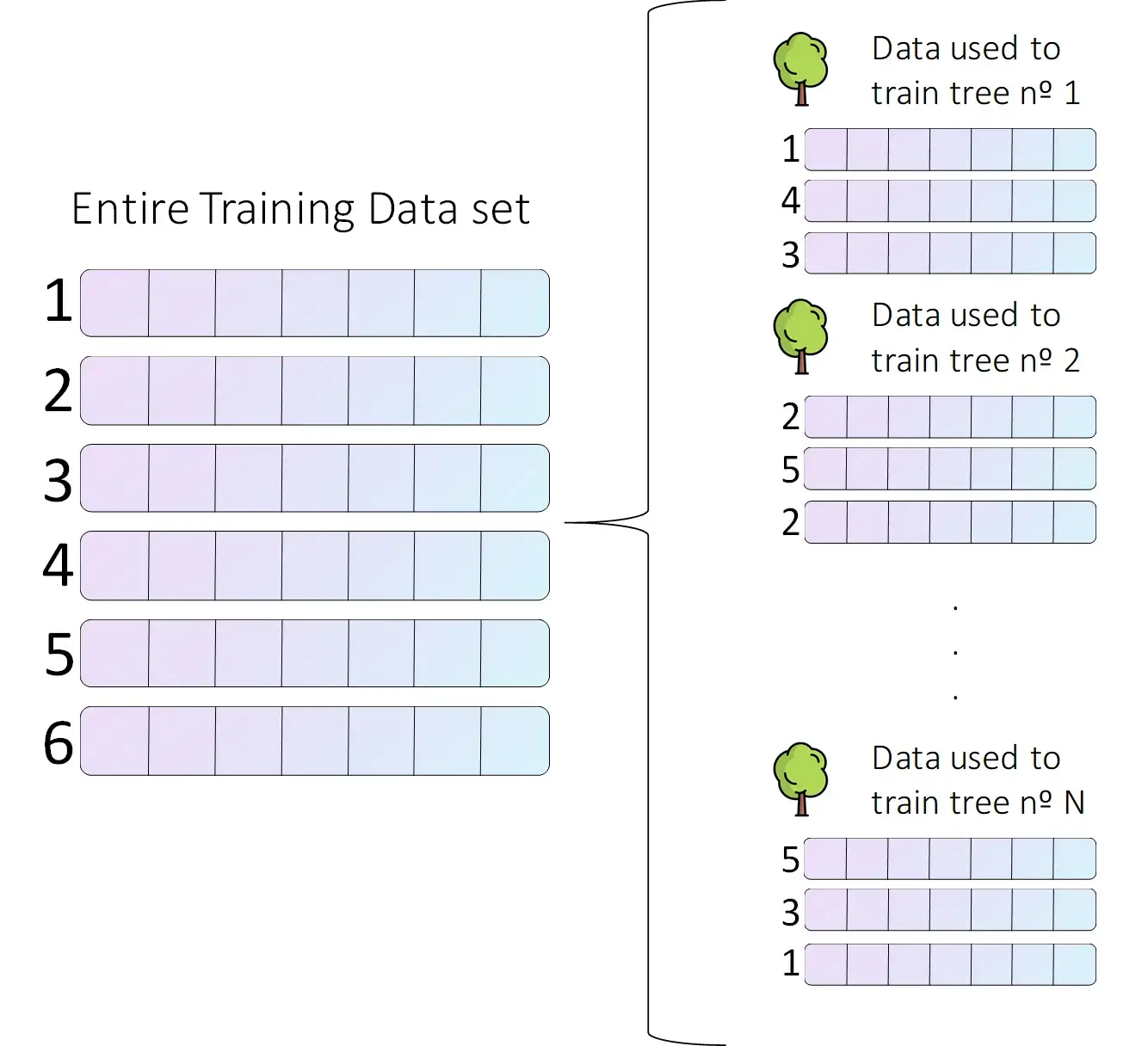
Глядя на этот рисунок, можно сделать различные выводы. Во-первых, размер данных, используемых для обучения каждого отдельного дерева, не обязательно должен быть равен размеру всего набора данных. Кроме того, точка данных может присутствовать более одного раза в данных, используемых для обучения одного дерева (как в дереве № 2).
Это называется выборка с заменой или бутстраппинг: каждая точка данных выбирается случайным образом из всего набора данных, и точка данных может быть выбрана более одного раза.
Используя различные выборки данных для обучения каждого отдельного дерева, мы уменьшаем одну из основных проблем, с которыми сталкиваются деревья: они очень любят свои обучающие данные. Если мы обучаем лес с большим количеством деревьев, и каждое из них было обучено на разных данных, мы решаем эту проблему. Все они очень любят свои обучающие данные, но лес не любит какую-то конкретную точку данных. Это позволяет нам выращивать более крупные отдельные деревья, поскольку мы уже не так сильно заботимся о том, чтобы отдельное дерево слишком хорошо подходило.
Если мы используем очень небольшую часть всего набора данных для обучения каждого отдельного дерева, мы увеличиваем случайность леса (уменьшая чрезмерную подгонку), но обычно ценой более низкой производительности.
На практике, по умолчанию большинство реализаций метода случайного леса (например, Scikit-Learn) выбирают выборку обучающих данных, используемых для каждого дерева, такого же размера, как и исходный набор данных (однако это не один и тот же набор данных, помните, что мы выбираем случайные выборки).
Как правило, это обеспечивает хороший компромисс между смещением и дисперсией.
Обучите лес деревьев, используя эти случайные наборы данных, и добавьте еще немного случайности при выборе признаков
Если вы хорошо помните, при построении индивидуального дерева решений в каждом узле мы оценивали определенную метрику (например, индекс Джини или информационное усиление) и выбирали признак или переменную из данных, которая должна быть в узле, минимизирующем/максимизирующем эту метрику.
Это хорошо работало при обучении только одного дерева, но теперь мы хотим получить целый лес таких деревьев! Как нам это сделать? Групповые модели, такие как модель случайного леса, работают лучше всего, если отдельные модели (отдельные деревья в нашем случае) некоррелированы. В методе случайного леса это достигается путем случайного выбора определенных признаков для оценки в каждом узле.
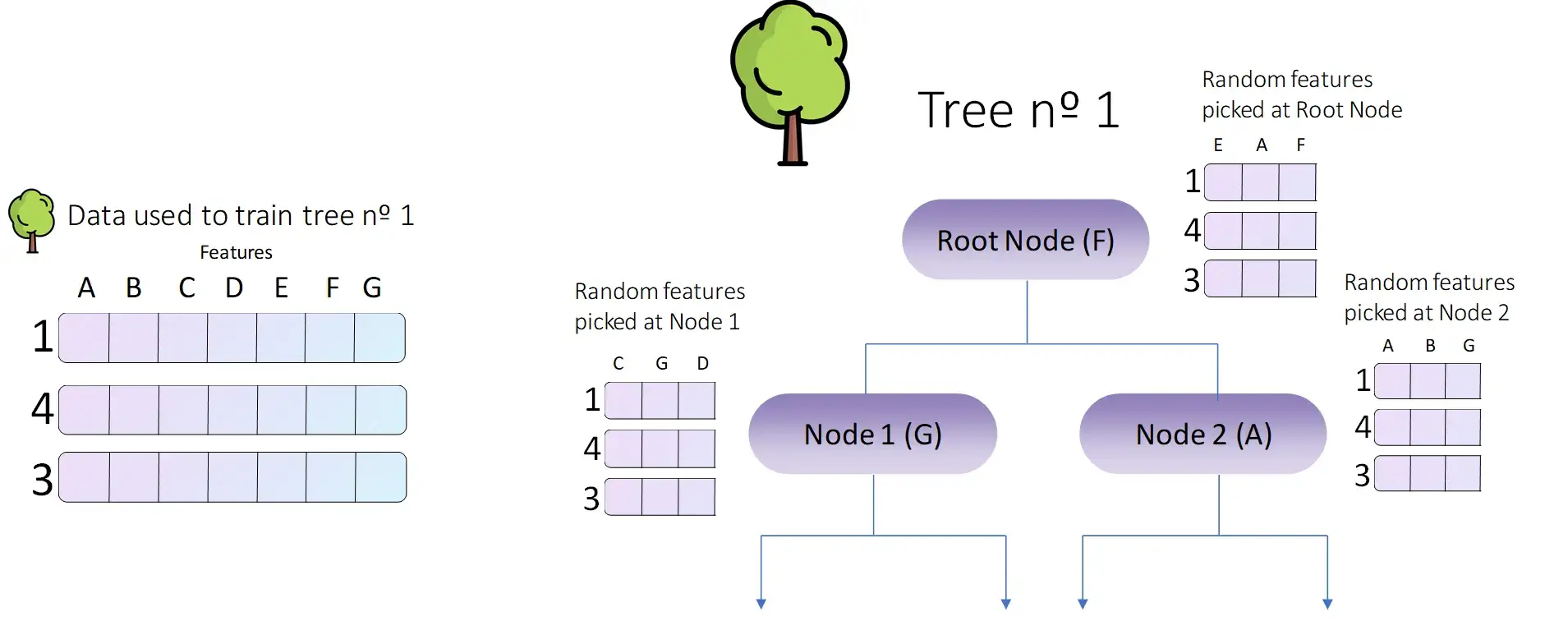
Как видно из предыдущего изображения, в каждом узле мы оцениваем только подмножество всех исходных характеристик. Для корневого узла мы учитываем E, A и F (и F побеждает). В узле 1 мы учитываем C, G и D (и G побеждает). Наконец, в узле 2 мы учитываем только A, B и G (и побеждает A). Мы будем делать это до тех пор, пока не построим все дерево.
Таким образом, мы избегаем включения признаков, обладающих очень высокой предсказательной силой, в каждое дерево, создавая при этом множество некоррелированных деревьев. Это второй прием случайности. Мы используем не только случайные данные, но и случайные признаки при построении каждого дерева. Чем больше разнообразие деревьев, тем лучше: мы уменьшаем дисперсию и получаем более эффективную модель.
Повторите это для N деревьев, чтобы создать наш удивительный лес.
Потрясающе, мы научились строить одно дерево решений. Теперь мы повторим это для N деревьев, случайным образом выбирая на каждом узле каждого из деревьев, какие переменные участвуют в конкурсе на выбор признака для разделения.
В итоге весь процесс выглядит следующим образом:
- Создайте бутстрапный набор данных для каждого дерева.
- Создайте дерево решений, используя соответствующий набор данных, но в каждом узле используйте случайную подвыборку переменных или признаков для разделения.
- Повторите все эти три шага сотни раз, чтобы создать массивный лес с большим разнообразием деревьев. Именно это разнообразие делает метод случайного леса намного лучше, чем одно дерево принятия решений.
Как только мы построили наш лес, мы готовы использовать его для создания потрясающих прогнозов. Давайте посмотрим, как это сделать!
Составление прогнозов с помощью случайного леса
Делать прогнозы с помощью случайного леса очень просто. Мы просто должны взять каждое из наших отдельных деревьев, пропустить через них наблюдение, для которого мы хотим сделать прогноз, получить прогноз от каждого дерева (суммируя N прогнозов) и затем получить общий, агрегированный прогноз.
Бутстраппинг данных и последующее использование совокупности для составления прогноза называется бэггингом, а способ составления прогноза зависит от типа проблемы, с которой мы сталкиваемся.
Для проблем регрессии совокупное решение - это среднее значение решений каждого отдельного дерева решений. Для задач классификации итоговое прогнозирование - это наиболее частое предсказание, сделанное лесом.
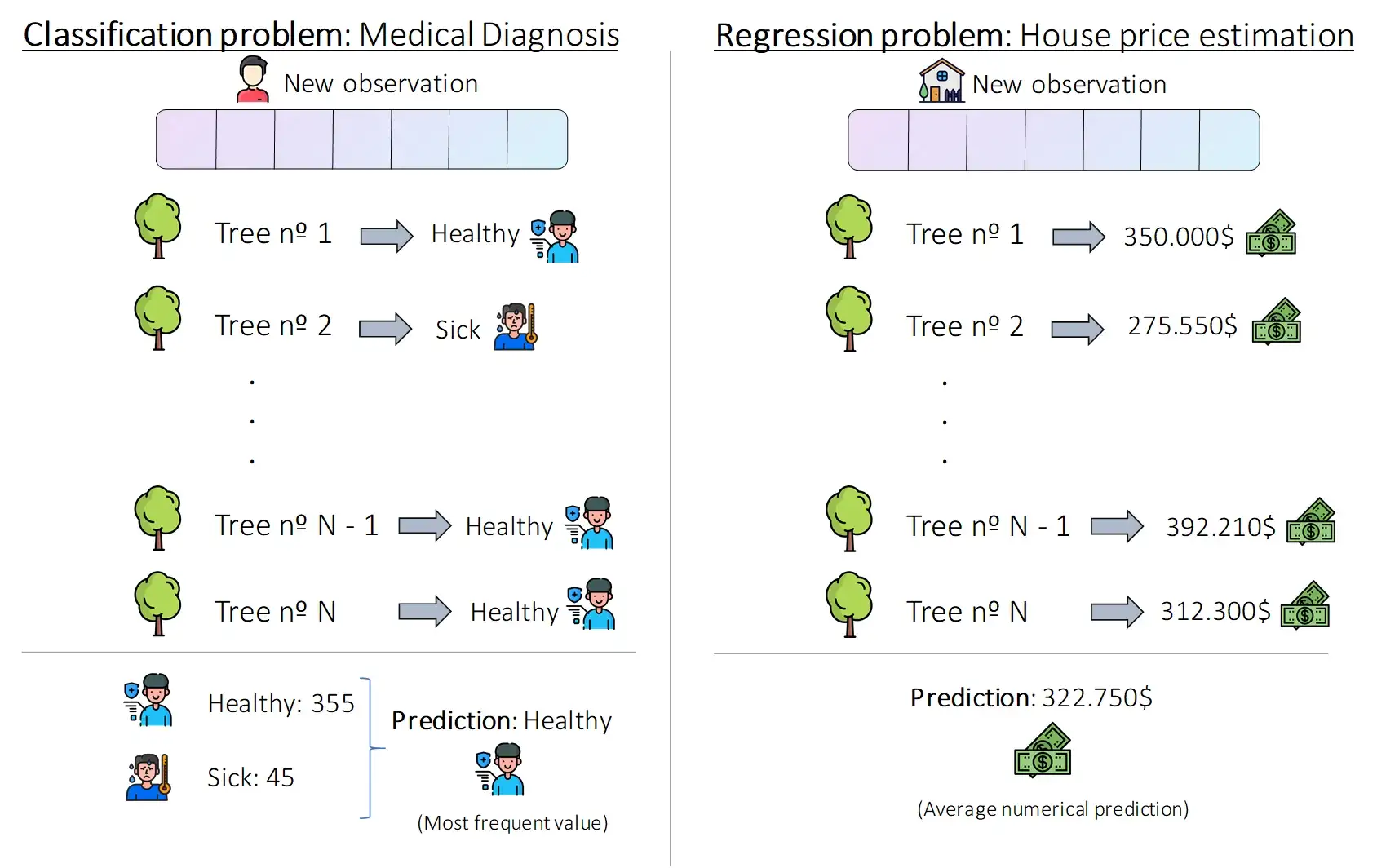
Предыдущее изображение иллюстрирует эту очень простую процедуру. Для задачи классификации мы хотим предсказать, болен или здоров определенный пациент. Для этого мы пропускаем его медицинскую карту и другую информацию через каждое дерево случайного леса и получаем N предсказаний (в нашем случае 400). В нашем примере 355 деревьев сообщают, что пациент здоров, а 45 - что болен, поэтому лес решает, что пациент здоров.
В задаче о регрессии мы хотим предсказать цену определенного дома. Мы пропускаем характеристики этого нового дома через N деревьев, получая от каждого из них числовое предсказание. Затем мы вычисляем среднее значение этих предсказаний и получаем окончательное значение 322,750$.
Просто, правда? Мы делаем прогноз по каждому отдельному дереву, а затем объединяем эти прогнозы, используя среднее значение (average) или режим (mode) (наиболее частое значение).
Заключение и другие ресурсы
В этой статье мы рассмотрели, что такое случайный лес, как он преодолевает основные проблемы деревьев решений, как они обучаются и используются для прогнозирования. Это очень гибкие и мощные модели машинного обучения, которые широко используются в коммерческих и промышленных приложениях, наряду с бустинг-моделями и искусственными нейронными сетями.
В следующих статьях мы рассмотрим советы и рекомендации по использованию метода случайного леса, а также то, как их можно использовать для отбора признаков.
Вот и все! Как всегда, я надеюсь, что вам понравился эта статья.
Большое спасибо, что читаете, и хорошего дня!

